paper-reading-group

Adversarial Machine Learning

Adversarial Machine Learning by definition is the fooling of a model of by giving it malicious input. Attacking a model is the process of crafting these malicious inputs. In general there are two types of adversarial attacking strategies, targeted and un-targeted. Un-targeted attacks are easier and are more successful in achieving their objectives but Targeted attacks are potentially more devastating as you can ‘control’ the output for any malicious activity. Further these attacks can be black-box or white-box. The attacks can be made on supervised learning, un-supervised learning (Biggio et al 2013) and reinforcement learning (Huang et al. 2017) as well, however for this session our focus will be on attacking supervised methods and white box attacks and discussing :

https://arxiv.org/pdf/1908.07125.pdf

https://arxiv.org/pdf/1712.06751.pdf

Given any model F such that it maps some input X to some output Y.

\[F(X)=Y\]

Attack is defined as another function G such that

\[G(X) = X'\] \[F(X')=Y' \ \ | \ \ Y' \neq Y\]

For a targeted attack you have a particular mapping for $Y$ → $Y’$

The other important aspect for any adversarial perturbation is how deceptive an attacker is, otherwise theoretically if you replace the entire instance with an actual different sample. So we define another function $\psi(X,X’)$ which measures the distance between two samples. and a threshold $\epsilon$ and limit our function $G$ such that.

\[G(X)=X' \ \ \ | \ \ \ \psi(X,X') \leq \ \epsilon\]

Adversarial NLP : White-Box-Attacks [Hotflip]

Representation :

In text $X$ the $j^{th}$ character of the $i^{th}$ word is represented by $x_{ij} \in (0,1)^{

V

}$ a one hot vector, where $V$ is the set of alphabets.

\[X = [(x_{11},...x_{1n});...(x_{m1},...x_{mn})]\]

therefore one edit in the text can be represented by one manipulation or one ‘flip’ as a vector operation where flip of say a → b given by :

\[\vec{v}_{ijb} = (0,..;(0,..(0,..-1,0,..,1,0)j,..0)i;0,..)\]

where -1 and 1 are in the corresponding positions for the a-th and b-th characters of the alphabet, respectively, and x(a) = 1. A first-order approximation of change in loss can be obtained from a directional derivative along this vector and approximated as given $J(X,Y)$ is the obtained loss:

\[\bigtriangledown \vec{v}_{ijb} J(X,Y) = \bigtriangledown_x J(X,Y)^T. \vec{v}_{ijb}\]

We take the derivative to optimise the flip. This is a character level flip for word level flips V changes to the vocabulary. Limitation : Maximum length of word and text.

Universal Adversarial Triggers

Adversarial examples highlight model vulnerabilities and are useful for evaluation and interpretation. We define universal adversarial triggers: input-agnostic sequences of tokens that trigger a model to produce a specific prediction when concatenated to any input from a dataset.

For example, triggers cause SNLI entailment accuracy to drop from 89.94% to 0.55%, 72% of “why” questions in SQuAD to be answered “to kill American people”, and the GPT-2 language model to spew racist out- put even when conditioned on non-racial con- texts. Furthermore, although the triggers are optimised using white-box access to a specific model, they transfer to other models for all tasks we consider.

The Universal Attack

In a non-universal targeted attack, we are given a model $F$, a text input of tokens (words, sub-words, or characters) $t$, and a target label $y’$. The adversary aims to concatenate trigger tokens $t_{adv}$ to the front / end of $t$ such that

\[F(t;t_{adv}) = y'\]

For the attack to be universal we aim to search the trigger such that the loss over the complete model is minimal.

Given the definition of the terms as earlier adversarial tokens are defined as.

\[v_{adv} \ | \ \ min \ E(J(X;v_{adv},Y'))\]

Trigger Search

To start the trigger search of a given length we initialise the triggers as stop-words,

e.g. [‘the’, ‘the’, ‘the’] and obtain the loss to optimise the triggers . The problem with text perturbation is the fact that it is discrete, therefore instead of brute forcing the triggers we update the embeddings to obtain the tokens. The technique is inspired from HotFlip and is similarly based on a linear approximation of the task loss and update the embedding for every trigger token $e_{adv}$ to minimise the loss’ first-order Taylor approximation around the current token embedding.

\[e_{adv} \ \ \ | \ \ argmin \ [e'_i −eadv_i]^T∇e_{adv_i}J\]

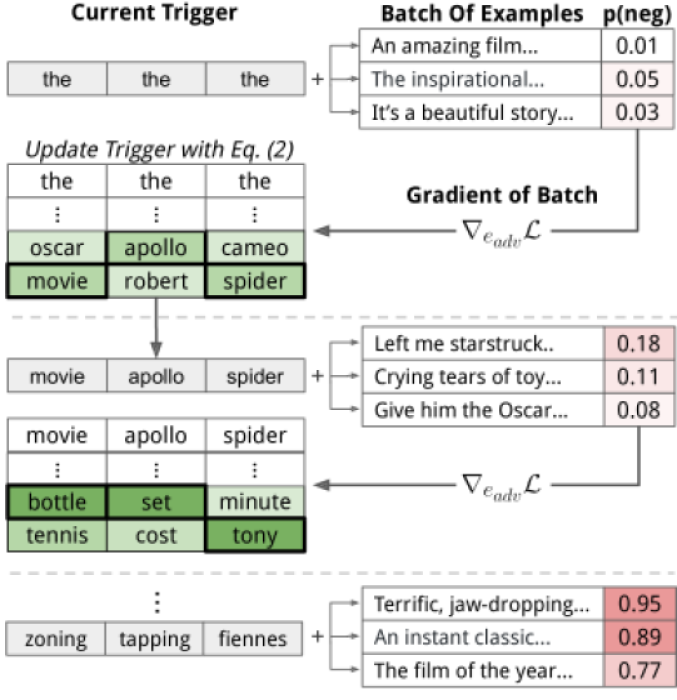
For targeted and un targeted attacks the algorithm can be as below :

averaged_grad = averaged_grad.cpu()
    embedding_matrix = embedding_matrix.cpu()
    trigger_token_embeds = (
        torch.nn.functional.embedding(
            torch.LongTensor(trigger_token_ids), embedding_matrix
        )
        .detach()
        .unsqueeze(0)
    )
    averaged_grad = averaged_grad.unsqueeze(0)
    gradient_dot_embedding_matrix = torch.einsum(
        "bij,kj->bik", (averaged_grad, embedding_matrix)
    )
    if not increase_loss:
        gradient_dot_embedding_matrix *= (
            -1
        )  # lower versus increase the class probability.
    if num_candidates > 1:  # get top k options
        _, best_k_ids = torch.topk(gradient_dot_embedding_matrix, num_candidates, dim=2)
        return best_k_ids.detach().cpu().numpy()[0]
    _, best_at_each_step = gradient_dot_embedding_matrix.max(2)
    return best_at_each_step[0].detach().cpu().numpy()

Since this process is not memory less we use beam search to optimise our search where a beam of a given size is evaluated at every step

Since this method requires a forward pass only it is computationally efficient.

References

1. Ebrahimi, Javid, et al. “Hotflip: White-box adversarial examples for text classification.” arXiv preprint arXiv:1712.06751 (2017).
2. Wallace, Eric, et al. “Universal adversarial triggers for attacking and analyzing NLP.” arXiv preprint arXiv:1908.07125 (2019).