paper-reading-group

MOPO: Model-based Offline Policy Optimization

Tianhe Yu, Garrett Thomas, Lantao Yu, Stefano Ermon, James Zou, Sergey Levine, Chelsea Finn, Tengyu Ma

https://arxiv.org/pdf/2005.13239.pdf

Problem:

• Offline RL: Regular RL methods need to improve with interaction. Not suitable for: generalization, safety, sample inefficient.
• Off-policy algorithms:
  • Model-free methods: Overestimation of Q function for out-of-distribution actions, Cannot generalise out of data’s states and actions.
  • Model-based methods: More supervised (since s,a rather than r), supervised training rather than RL, better uncertainty estimation techniques than value-based RL. But here model cannot be improved with experience, so need to be careful on what model learns.

Solution:

• Model where reward is penalized by model error (to account for model uncertainty). This is the MDP
• Train policy on this MDP using MBPO

Details:

• Use model based because of earlier specified reasons and that MBPO performs better than SAC off the shelf on D4RL
• MBPO
  • Learns transition and reward distribution (this is the model) from data
  • During training, use transition model to generate rollouts and save in replay buffer
  • Update policy using both model data and given data. (Like Behavioral Cloning, World models)
  • In online setting: Additionally use both model and environment to improve model and policy (Like Dyna)
• MOPO
  • Return: Should be able to generalize to OOD data. But Risk: model will become unreliable for OOD data and might overfit to unreliable model data. Need to balance these
  • Quantifying uncertainty: from dynamics to return
    • How does error in transition model affect error in return?
      • Note: Estimate true model using learned model. Estimate true return using return from model.
      • Lemma 1: Return depends on G (difference in values from both transition models). A model that gets high reward and minimizes G will maximize return on real model too. If we can get G, can use as upper bound for return.
      • Since V is unknown, replace with terms depending only on transition model. Options depend on assumptions we take.
        • If assume that reward is bounded can write Eq. 4 (Simpler assumption)
        • If assume V’s are Lipschitz functions, can use Wasserstein distance and write Eq 5
  • Algorithm 1: With Eq 4. assumption.
    • Penalize reward by an amount proportional to model error (T error). From Eq. 2
    • Run till convergence: policy = argmax (estimated return).
  • Algorithm 2: With Eq. 5 assumption
    • This is final MOPO since Lipchitz regularization has been seen to improve in and out of distribution generalization.
    • Uncertainty is quantified using maximum standard deviation of model prediction from Lipchitz regularized mean.

  

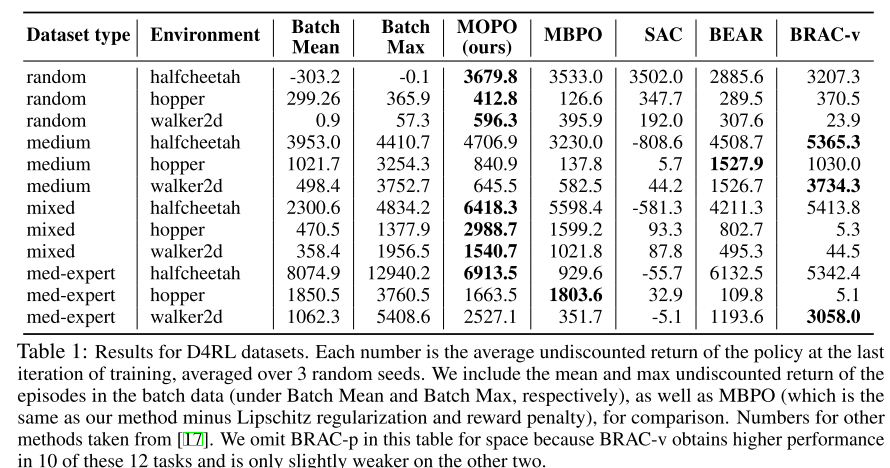
Results

• In distribution, for different dataset categories
  • random - random policy
  • medium - partial SAC then rollout
  • mixed - SAC then take replay buffer as dataset
  • medium-expert - combine fully trained policy with rollouts from either partial or random

• Out of distribution generalization
  • Cheetah-jump - Train on walk, test on jump
  • Ant-angle - Train on straight walk, test on 30 degree walk

Future work

• Don’t theoretically understand why model-based perform so much better on offline tasks. Find out why.
• Find how to get model-free offline methods up to the level of model-based.