paper-reading-group

Model Based Reinforcement Learning

Motivation

• Every living being — carries a model of external reality
  • Small and Long term simulations based on actions and imagination of next states.
• Benefits?
  • More Scenarios
  • Safer and more competent
  • Simulate expensive/not safe “real” world scenarios with little data.
  • Have models of other agents in the world (e.g. in the case of self-driving scenarios)
• AlphaGo
  • Search over different possibles of the game. Plan better.
• Used a lot in:
  1. Self-driving
  2. Robotics and Control
  3. Game play (alphago)
  4. Operations Research (energy)

  And many more

Problem Statement

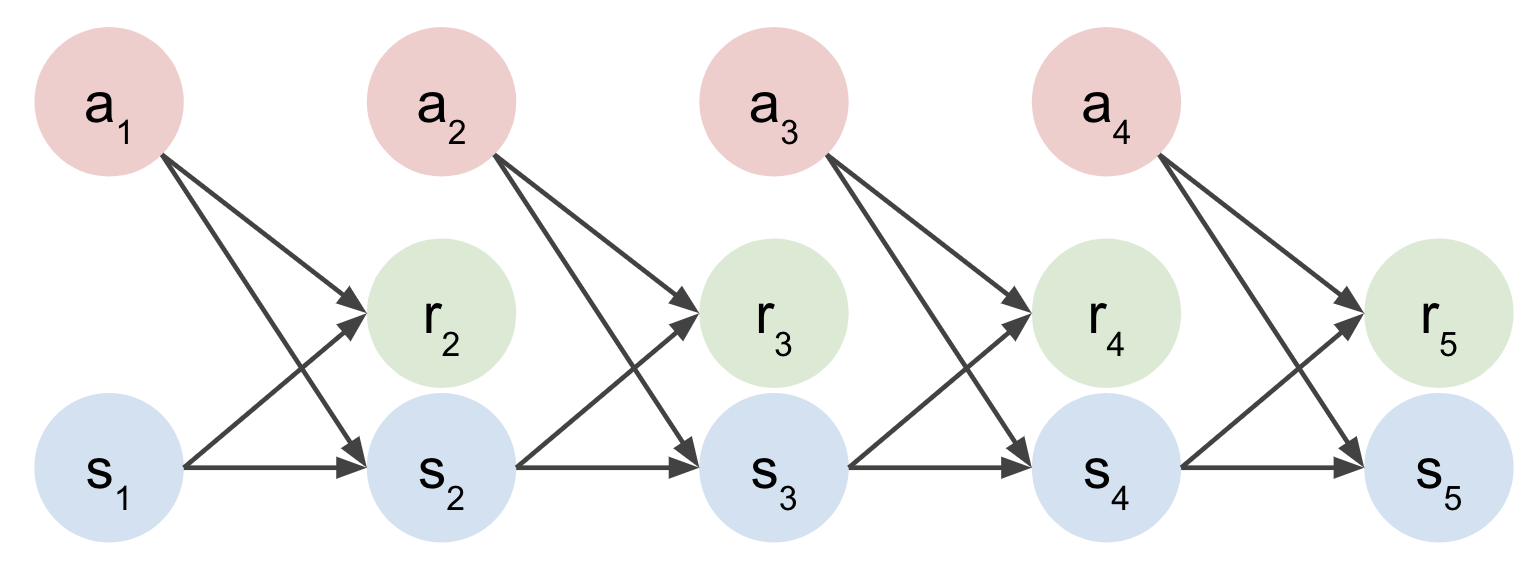
Markov Decision Process

\[(S, A, f, r) \\ where\ S\ is\ the\ State\ Space\\ A\ is\ the\ Action\ Space\\ T\ :\ S\ \times A\ \rightarrow \ S\ is\ a\ deterministic\ state\ transition\ function\\ r : S \rightarrow \R\ is\ the\ reward\ function\\ \gamma\ \epsilon\ (0,1)\\ Policy\ \pi\ :\ S\ \rightarrow\ A\]

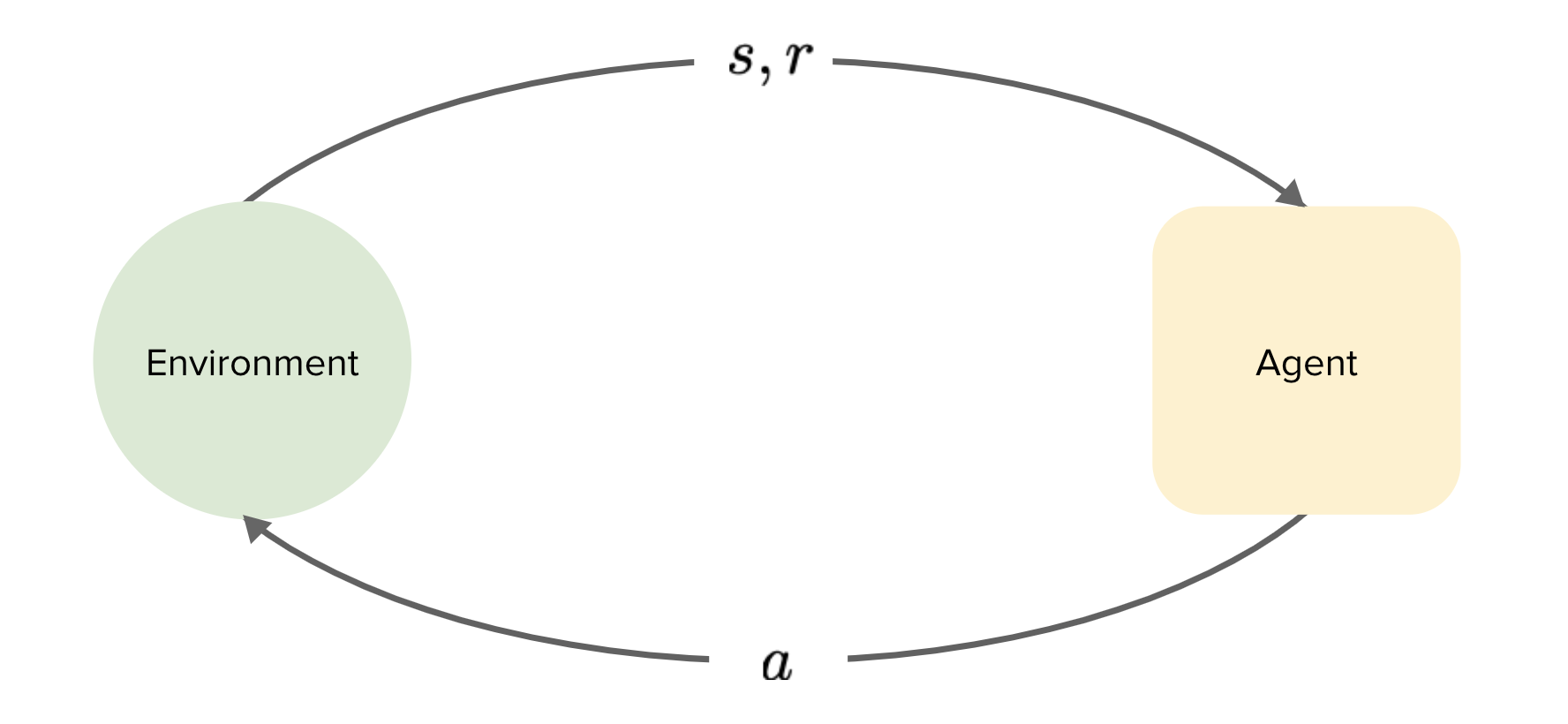
Model-free vs Model-based RL

First:

• Collect data: $D \rightarrow {s_{t}, a_{t}, r_{t}, s_{t+1}}$

Model-free:

1. Learn policy directly form data.

$D \rightarrow \pi$

Model-based

1. Learn Model of the world
2. Use this model to improve or learn a policy

$D \rightarrow f \rightarrow \pi$

What is the model?

Model is a representation that explicitly encodes knowledge about the structure of the environment and task.

1. Transition/Dynamics Model: $s_{t+1} = f_s(s_t, a_t)$
2. A model of the rewards:  $r_{t+1} = f_r(s_t, a_t)$
3. An inverse transition/dynamics model: $a_t = f_s^{-1}(s_t, s_{t+1})$
4. A model of distance
5. A model of future rewards.

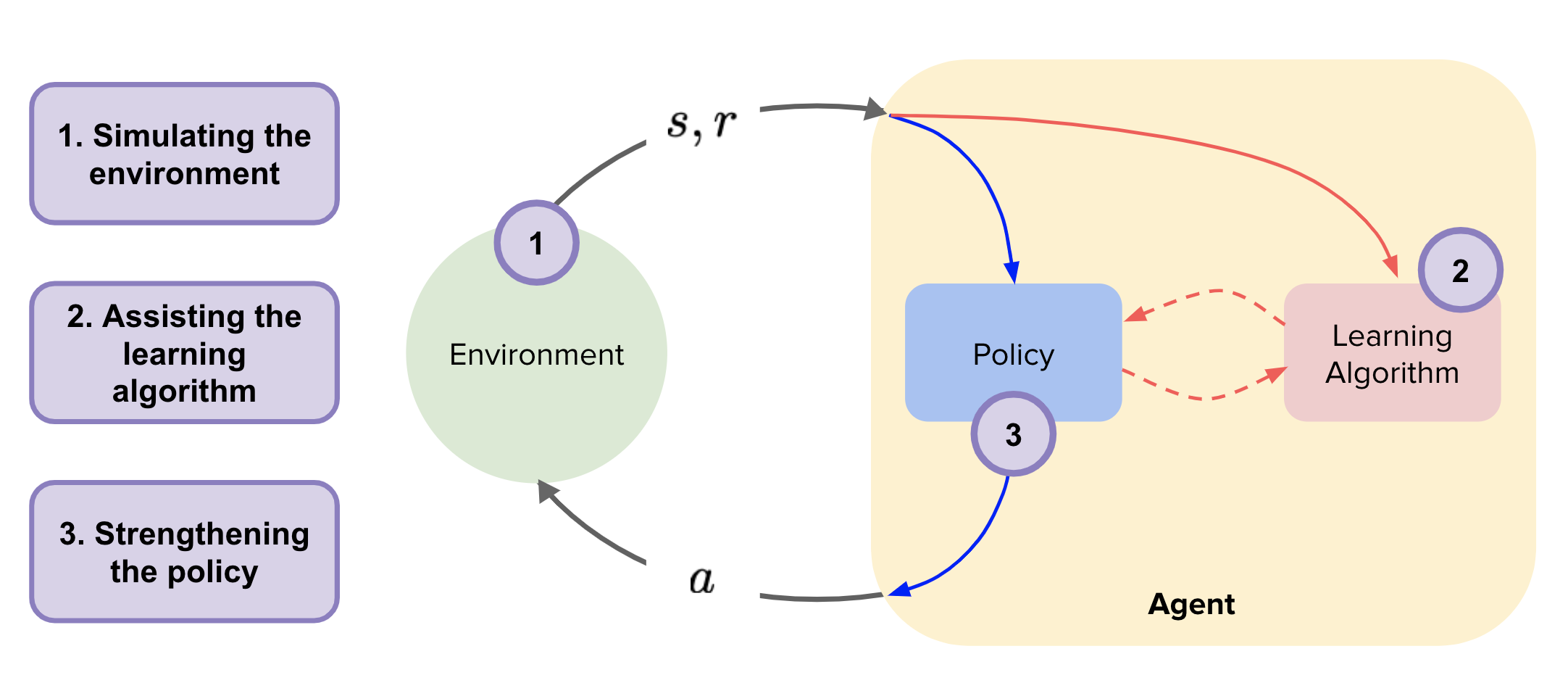
Where does the model fit?

Transition Models

• State Based
• Observation Based
• Latent State Based

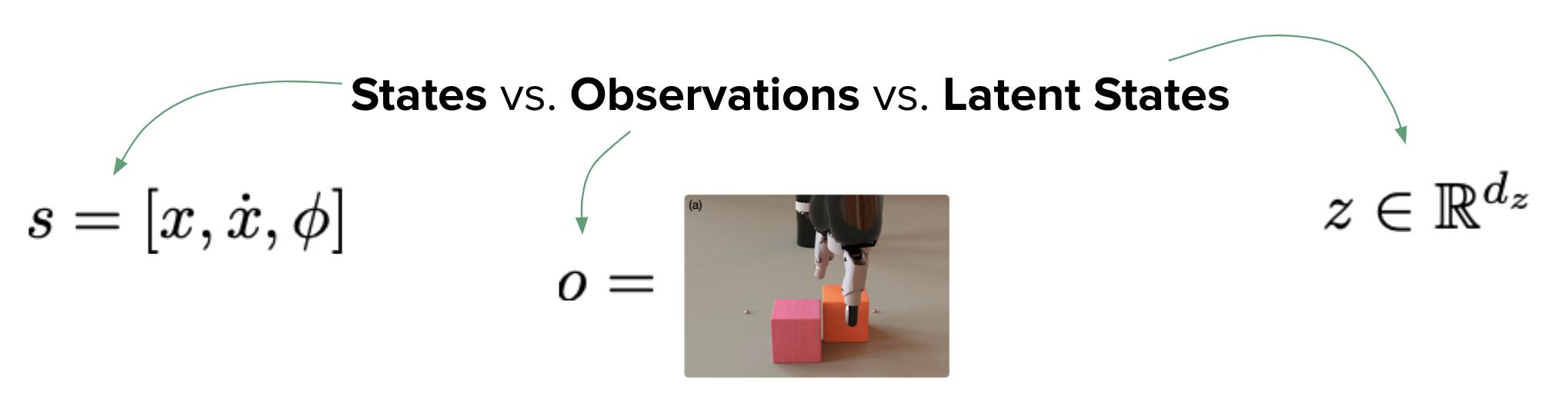
State-based Transition Model

Assumption: MDP is fully observable. All physics (if there is) is also assumed to be known.

• Train directly on states

Other approaches

• Represent state variables as nodes in a GNN - high inductive bias

What if we dont have states but only observations?

e.g. Images

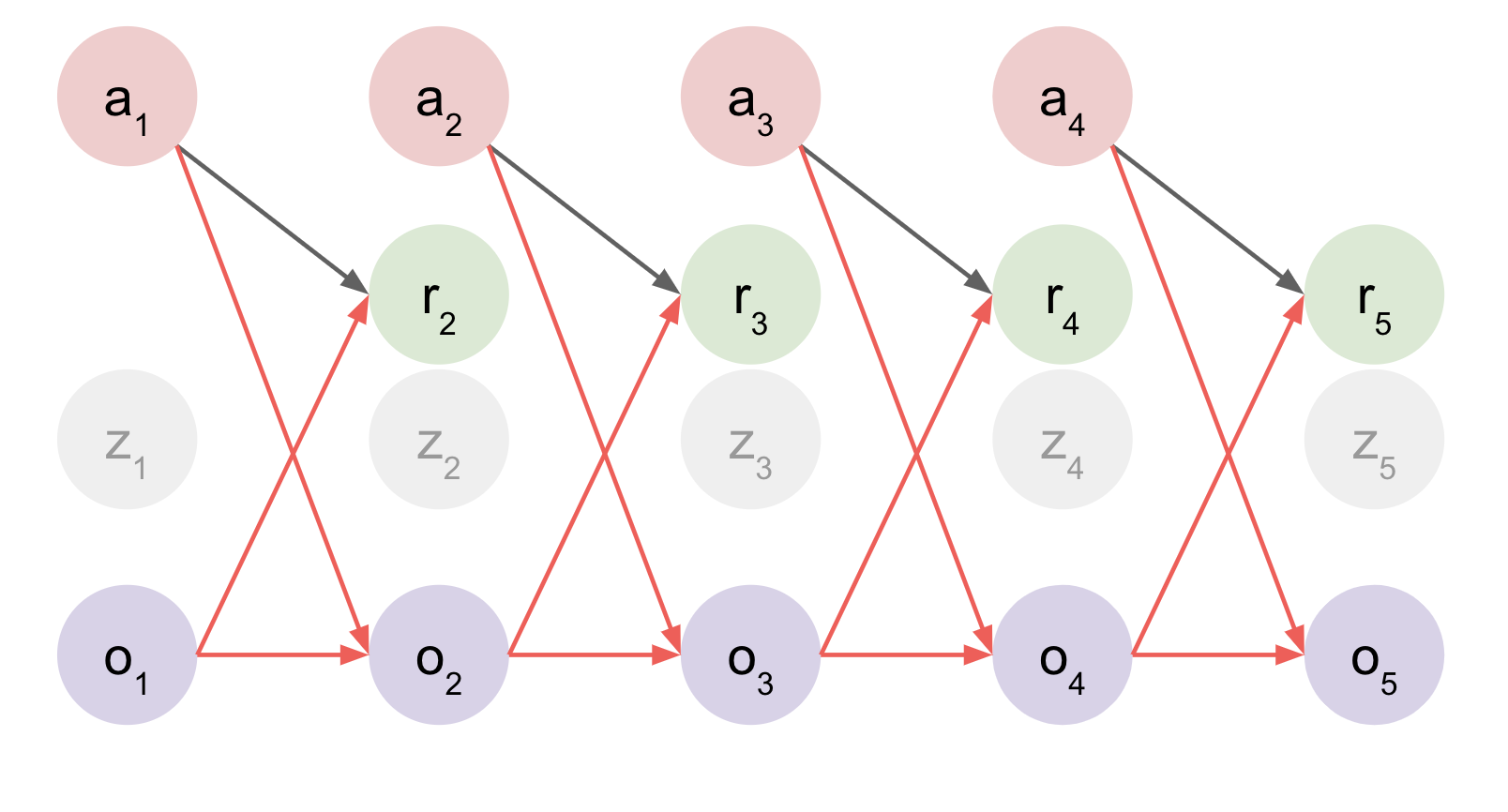
• Observation Transition Model $o_{t+1} = f_o(o_t, a_t)$
• Reconstruct observations at each timestep? (from Latent State)
  • Works well![5]

Problems:

1. Reconstruction at every timestep is great but VERY expensive.

Latent State Based

• Embed Initial Observation and rollout in a latent space.

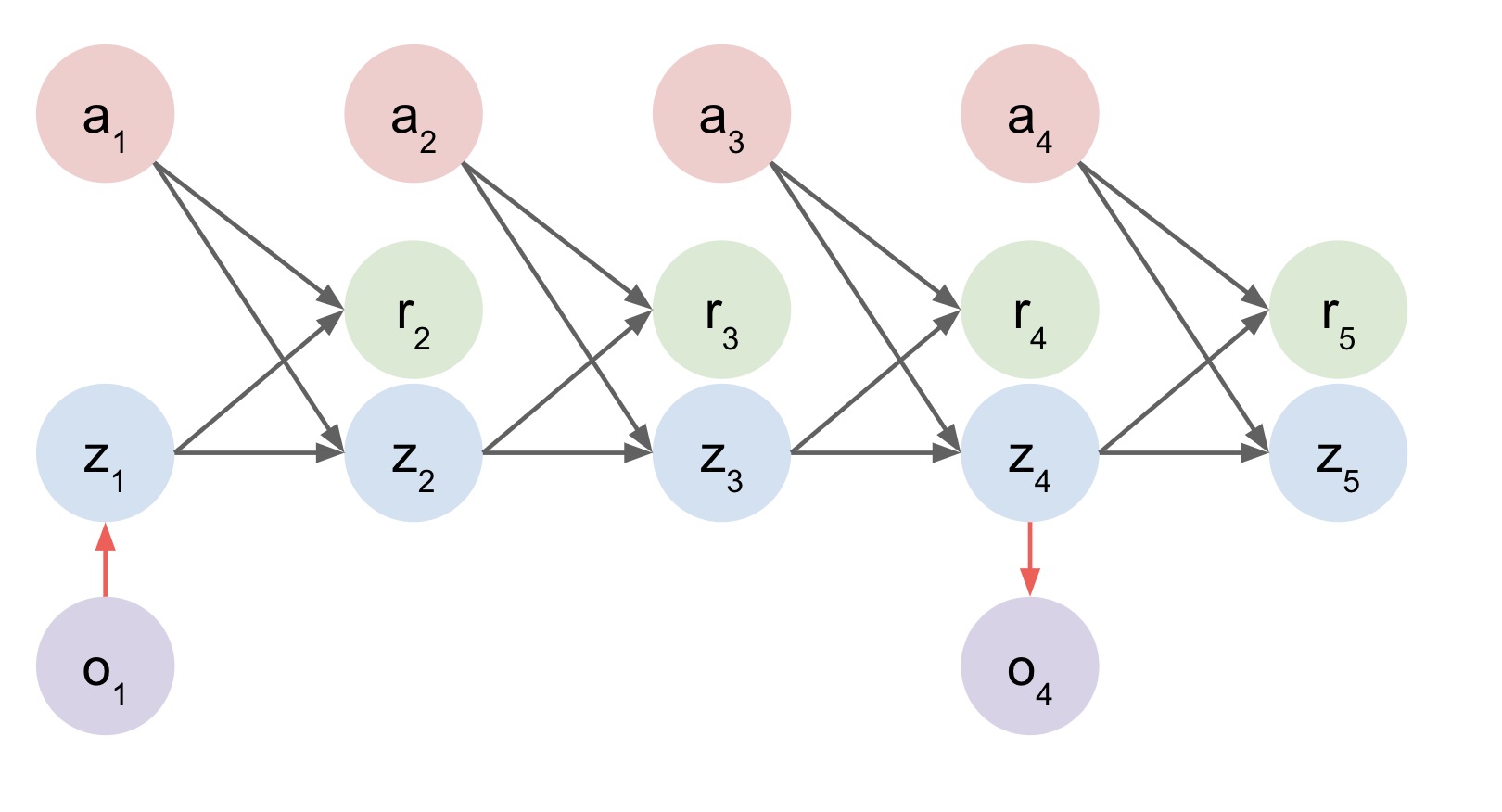
Latent Space Models

Examples:

1. World Models (Ha and Schmidhuber)[6]
2. PlaNet[7]
3. Dreamer[8]

Do you have domain knowledge?

1. Structure your deep learning models in an advantageous way.
   1. E.g. Object Oriented Learning[9]

Recurrent Value Models

• Predicting Value Function at each timestep.
• Essentially imagine expected return.

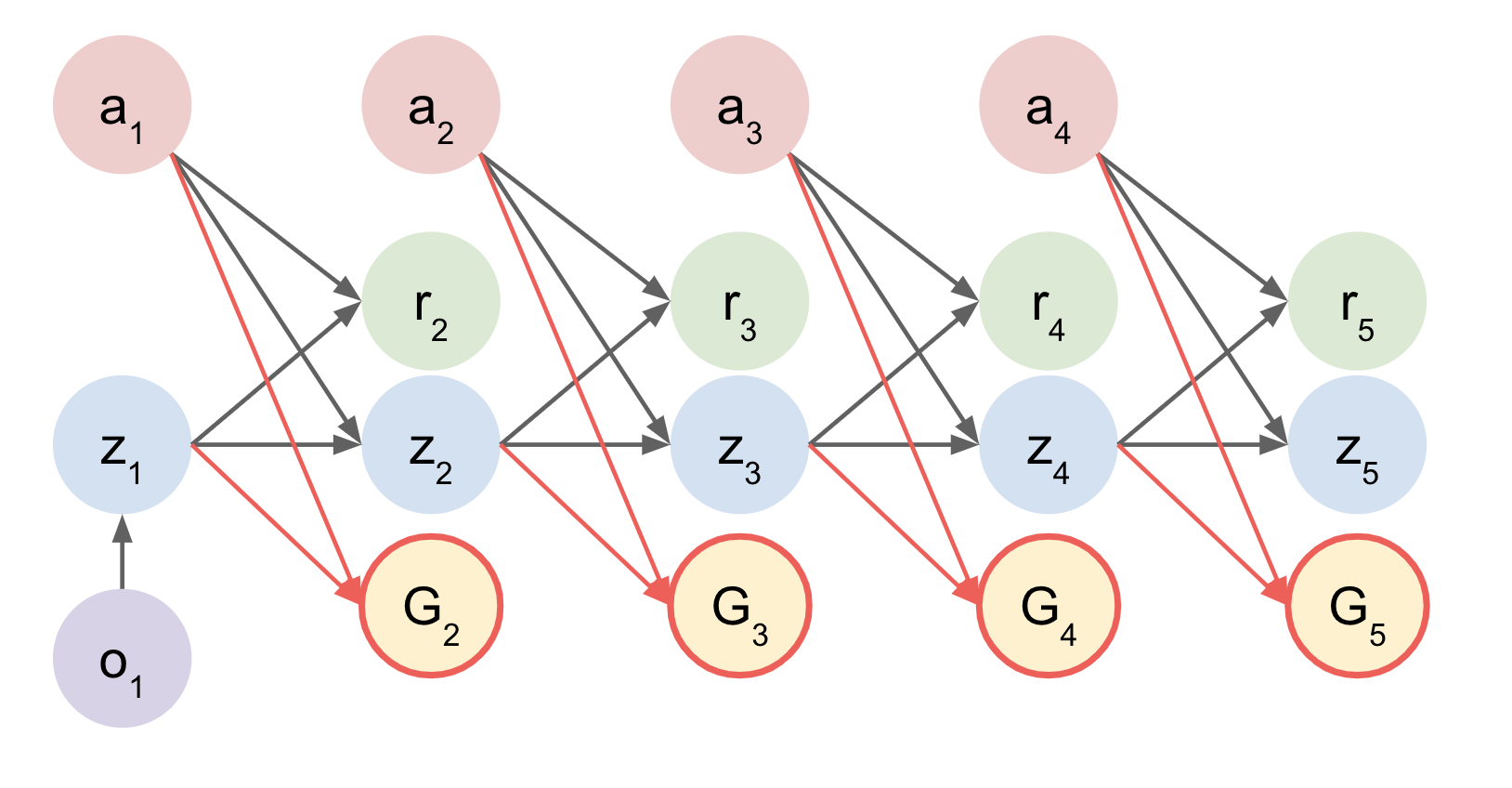
Imagined Value Function

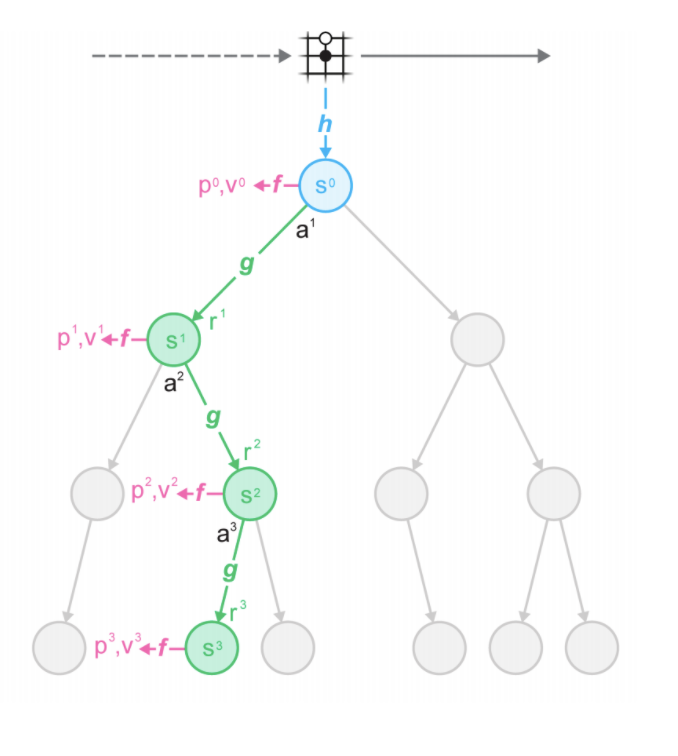
MCTS based search over states. To select best action at each timestep.

Tradeoffs of representing states.

Non-parametrics methods

• Represent transitions using graphs?
  • Works well! Memory Constraints!
• Simply use replay buffers?
  • Works well! Memory Constraints!
• Symbolic Descriptions of “plans” using PDDL[10]
  • Accurate plans but not scalable.
• Use Gaussian Processes to represent transitions
  • Really good at uncertaininty estimation (rare events for e.g. when caring about safety)

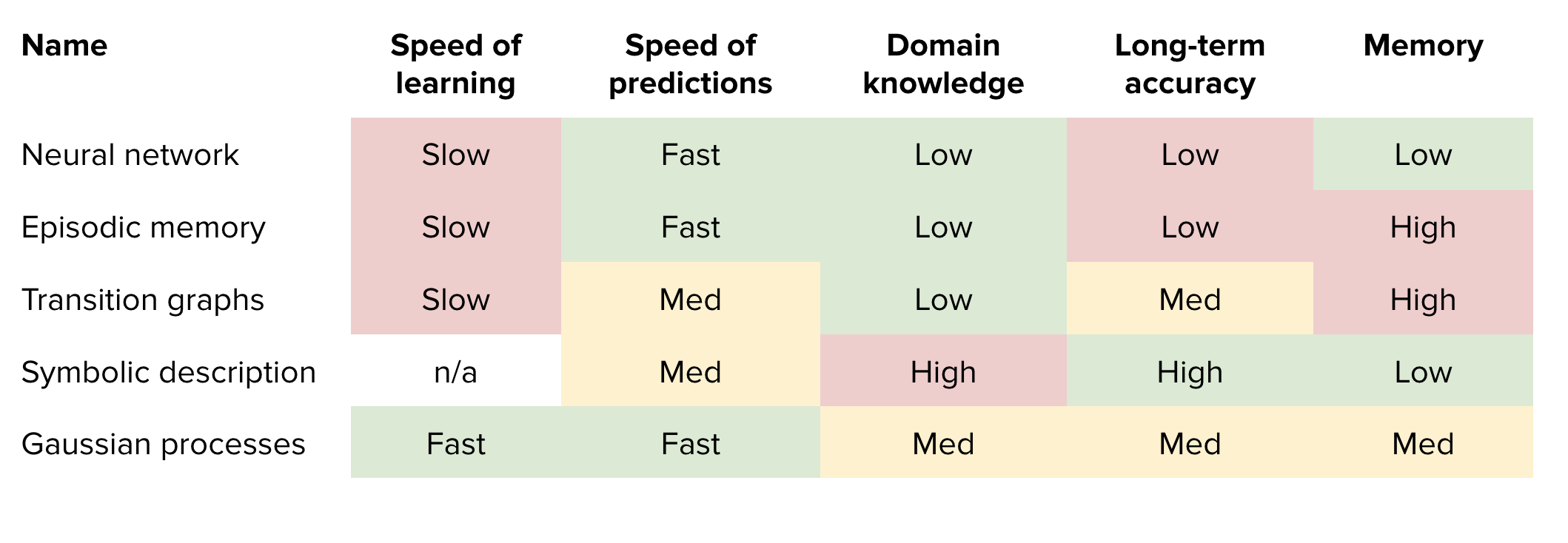
Tradeoffs for ways to model transitions.

What after having a model?

• Revisiting original landscape

Where does the model fit?

Simulate the Environment

1. Mix Model-generated experience with real data.
2. Similar to data augmentation of the whole environment
3. Dyna-Q (Sutton): One of the seminal papers.
   1. Idea is to simulate next transitions at current state for the 1 timestep only.
4. MBPO:
   1. Extension to n-timesteps.
   2. Advantage: Better exploration (as more possible trajectories are covered), especially helpful in robotics since data collection is expensive and costly (in terms of safety)

Assisting Policy Learning

Why?

• End to end training of model + planning + execution.

Whats wrong with traditional gradient application?

E.g. Reinforce

1. High Variance! Means model gradients are very noisy, making training worse and worse

What do we do?

• Replace transition functions of env with model

Revisiting Policy Gradient:

\[J(\theta) = \sum\gamma^tr_t\]

Recall reward definition of model:

\[r_t = f_r(s_t, a_t)\]

Plugging in and using chain rule:

\[J(\theta) = \sum\gamma^t( \nabla_sf_r(s_t, a_t)\nabla_\theta s_t + \nabla_af_r(s_t, a_t)\nabla_\theta a_t)\]

• BPTT!

Here again, gradient of states wrt model parameters can be replaced from the state transition functions. Should be easy to extend :)

Characteristics[1]:

• Deterministic (No variance) ✅
• Long-term credit assignment ✅
• Prone to local minima ❌
• Poor conditioning (Vanishing/Exploding Gradients) ❌

Strengthening the Policy

Refer 1.

Notes

References

1. ICML Tutorial on Model-based RL: https://sites.google.com/view/mbrl-tutorial
2. Model Predictive Control: http://papers.nips.cc/paper/8050-differentiable-mpc-for-end-to-end-planning-and-control.pdf
3. Cross Entropy Method for Action Selection in Model Based RL : https://arxiv.org/pdf/1909.12830.pdf
4. AlphaGo: https://www.nature.com/articles/nature16961
5. Visual foresight: Model-based deep reinforcement learning for vision-based robotic control.: https://arxiv.org/pdf/1812.00568.pdf
6. World Models https://arxiv.org/abs/1803.10122
7. PlaNet https://arxiv.org/abs/1811.04551
8. Dreamer: https://ai.googleblog.com/2020/03/introducing-dreamer-scalable.html
9. Object Oriented Learning: https://oolworkshop.github.io/
10. From Skills to Symbols: Learning Symbolic Representations for Abstract High-Level Planning
11. Dyna-Q: Dyna, an integrated architecture for learning, planning, and reacting. Chapter 9, Reinforcement Learning (Sutton and Barto)
12. When to Trust Your Model: Model-Based Policy Optimization.: https://arxiv.org/abs/1906.08253