paper-reading-group

Lottery Ticket Hypothesis

Neural Network pruning. But currently sparse networks cannot be trained from scratch.

Question: Why arent pruned networks trained from scratch?

The Hypothesis

Lottery Ticket Hypothesis: Dense, randomly-initialized, feed-forward networks contain subnetworks (winning tickets) that when trained in isolation reach test accuracy comparable to the original network in a similar number of iterations.

Algorithm 1: Pruning

1. Randomly initialize a neural network: $f(x; \theta_{0}) \ where \ \theta_{0} \text{\textasciitilde} D_{\theta}$

2. Train the network for $j$ iterations
3. Prune $p \%$ of the network (through some algorithm).
4. Reset the remaining weights to values in $\theta_{0}$, and hence the winning ticket $f(x;\ m \bigodot \theta_{0})$ .

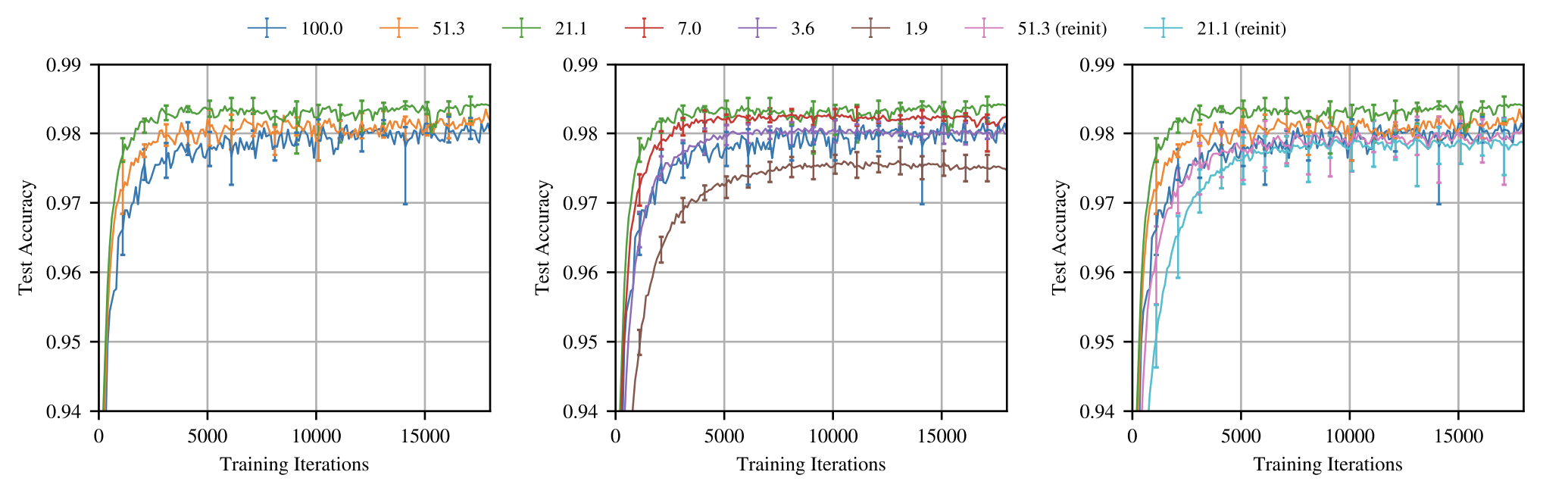
Figure 1: The legends represent Sparsity mask = 1 - Percentage of weights pruned. So 100% sparsity mask correspondings to 0% weights pruned. Pruned network performance with sparsity mask 21% is highest.

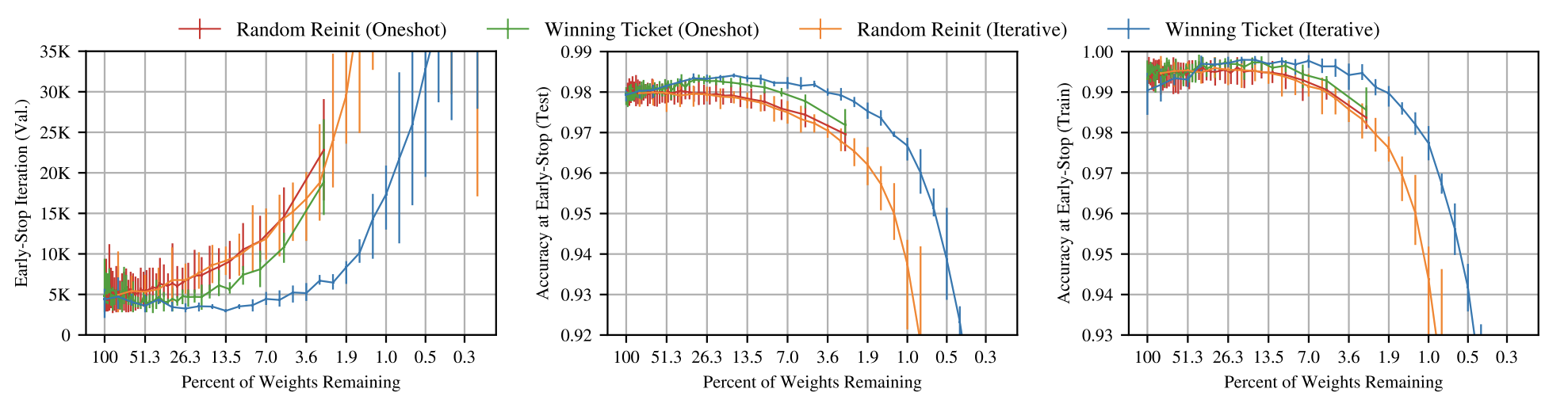
Figure 2: Early stop iteration increases with higher sparsity.

Algorithm 2: Iterative Pruning

1. Perform a step of finding the lottery ticket and prune by 20%
2. Repeat

Algorithm 3: One Shot Pruning

1. Is essentially Algorithm 1.

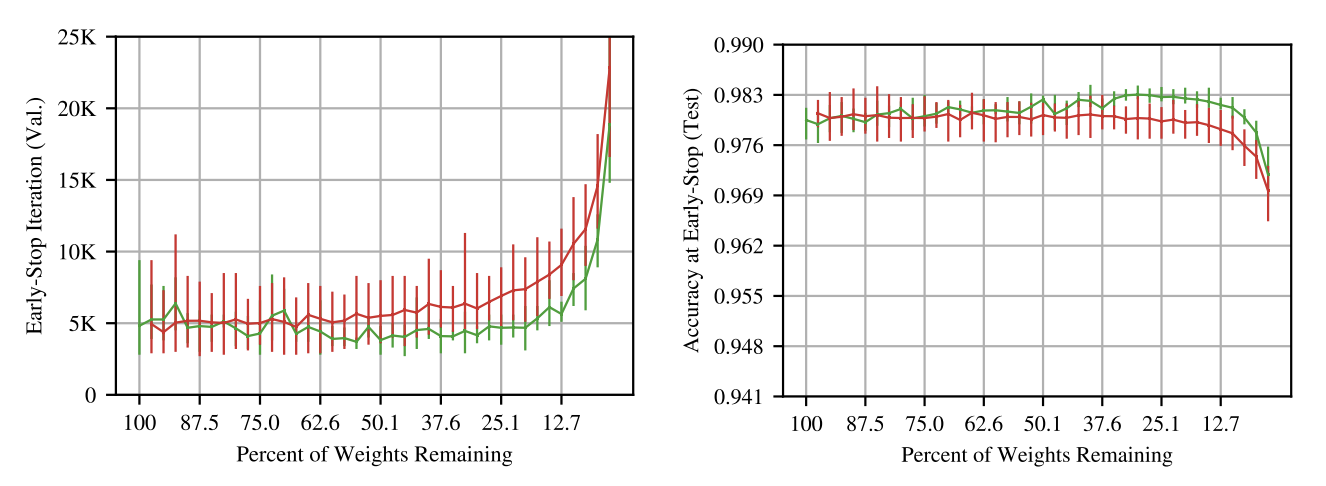
Figure 3: One shot pruned tickets are also winning tickets.

Convolutional Neural Networks

Whats the difference?

1. Shared weights. Hence computation is very sensitive.

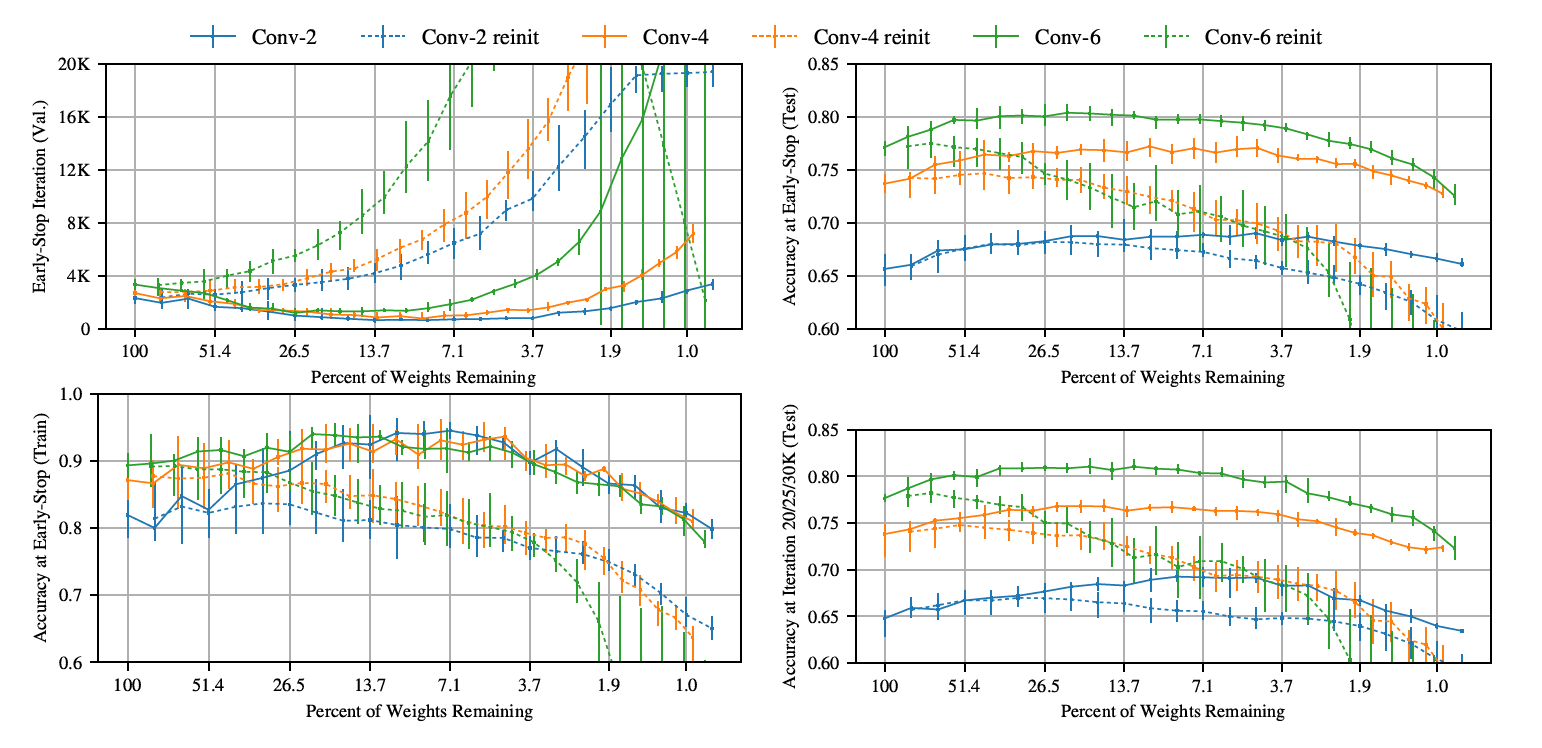
Figure 4: CNNs also have winning tickets!

Dropout

Whats the difference?

1. Connections are randomly removed during training.

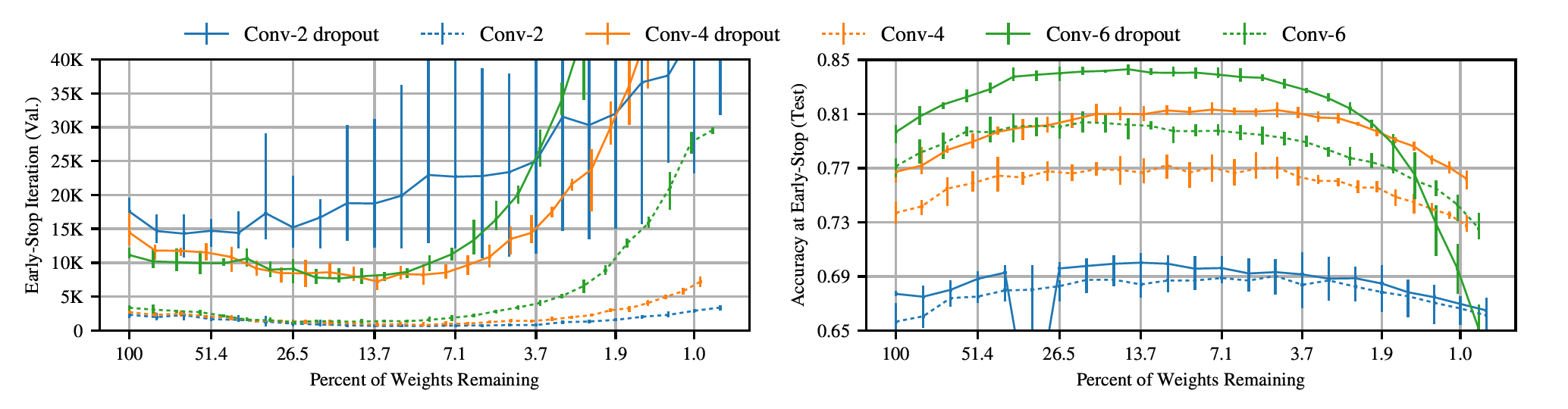
1. Better winning tickets than even usual ones. (Rigging the lottery).

Discussion

1. Do these tickets come from having the same initial distribution as the final one? No. Check Appendix F.
2. Reinitializing to the same distribution is almost the same as having an inductive bias.
3. Winning tickets exceed performance of original tickets? A very known result even in the literature surrounding Quantized networks perform better than original overparameterised networks.

4. Deeper networks require learning rate warmup.

   

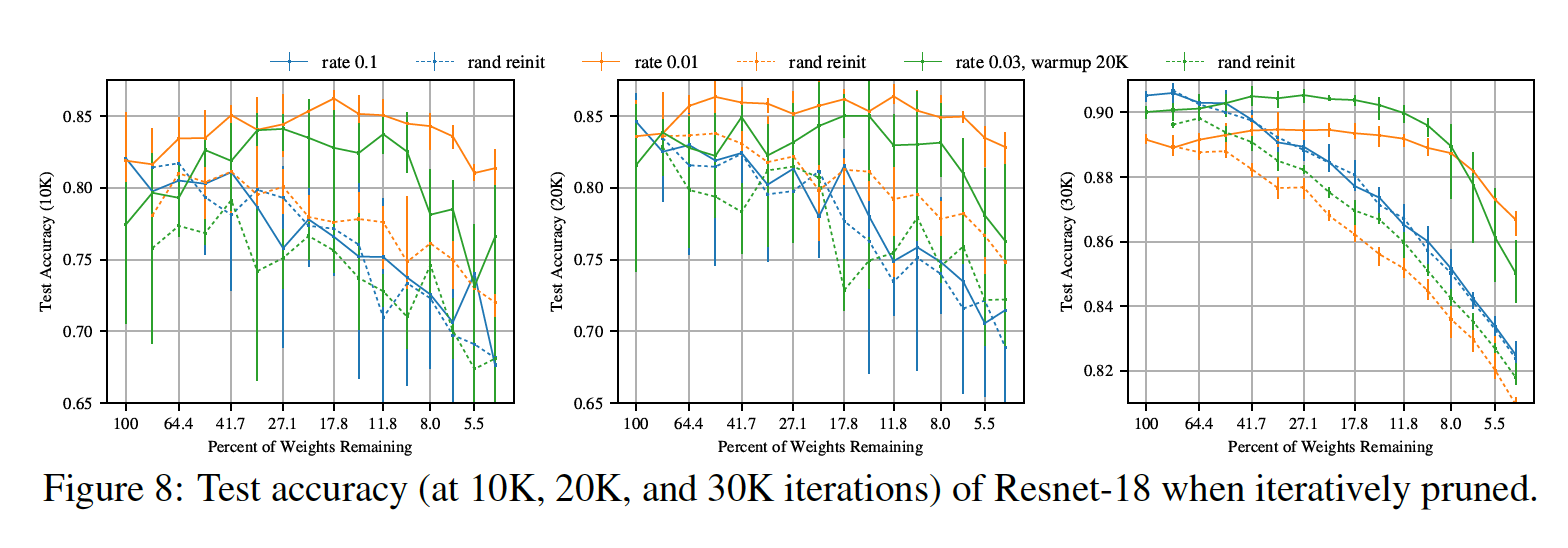
Future work

1. Structured pruning
2. Non-magnitude based pruning
3. Extension to Language Models