paper-reading-group

Graph Neural Networks

Graphs

A Simple Graph:

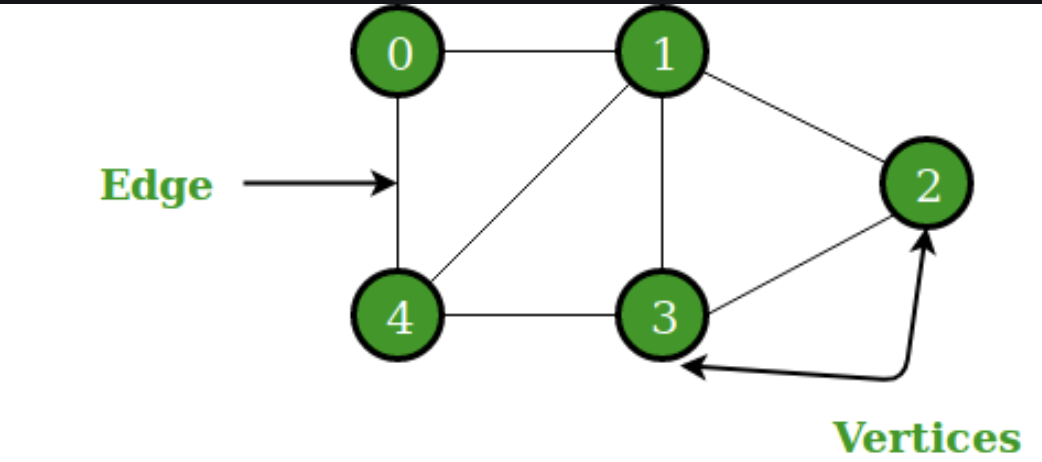
Figure 1: A Simple Graph

Graphical Communities:

Figure 2: Community Graphs

Etc.

When to use Graph Neural Networks?

1. Some interaction between graphical entities is required and an embedding representation will be better. Some Examples :-
   1. Social Network Relationships.
   2. Textual Relational Reasoning.
   3. Interaction Prediction
   4. Chemistry/Biology/etc

Graph Neural Networks

Basic definitions

1. A Graph (V, E). Often represented through the adjacency matrix i.e., (V, V).
2. Nodes can have two features:
   1. Some features of its own:- attributes, embedding, etc
   2. Related nodes, position in the graph, etc.
3. Edges:
   1. Direction
   2. Weight

Goal

1. For every node v, we would like to develop a representation (embedding) $h_{v} \ \epsilon\ \Reals^{d}$
2. Once we have $h_{v}$, it can be used for other downstream tasks like node classification, community detection, graph embedding, etc.

DeepWalk

1. Recap of skip-gram:
   1. Given a sequence of words: $W_{1}^{n} = (w_0, w_1, …., w_n)\ where\ w_i \epsilon\ V$

   2. We would like to maximize the $P(w_n

      \ w_0, w_1, …, w_{n-1})$

2. How do we transfer this approach to Graphs?
   1. Perform Random Walks on the graph.
   2. How do we relax random walks so that it can work with huge length walks?

      1. Minimize $-log P({w_{i-w},…., w_{i+w}

         \Phi (v_{i}) }$

3. Unsupervised
4. Things that could be added:
   1. Loss which induces better embeddings
   2. Instead of walking, aggregation

Neighborhood Aggregation

1. A neighborhood aggregation function
   1. $h_{v} = f(x_v, x_{co[v]}, h_{ne[v]}, x_{ne[v]})$
   2. All have different weight matrices here^
2. Output function
   1. $o_v = g(x_v, h_v)$
3. Compute losses and train
   1. $\sum_{i=1}^{p} criterion(t_i, o_i)$
   2. Note: Not an sum, but a average.

4. Generate embeddings

   

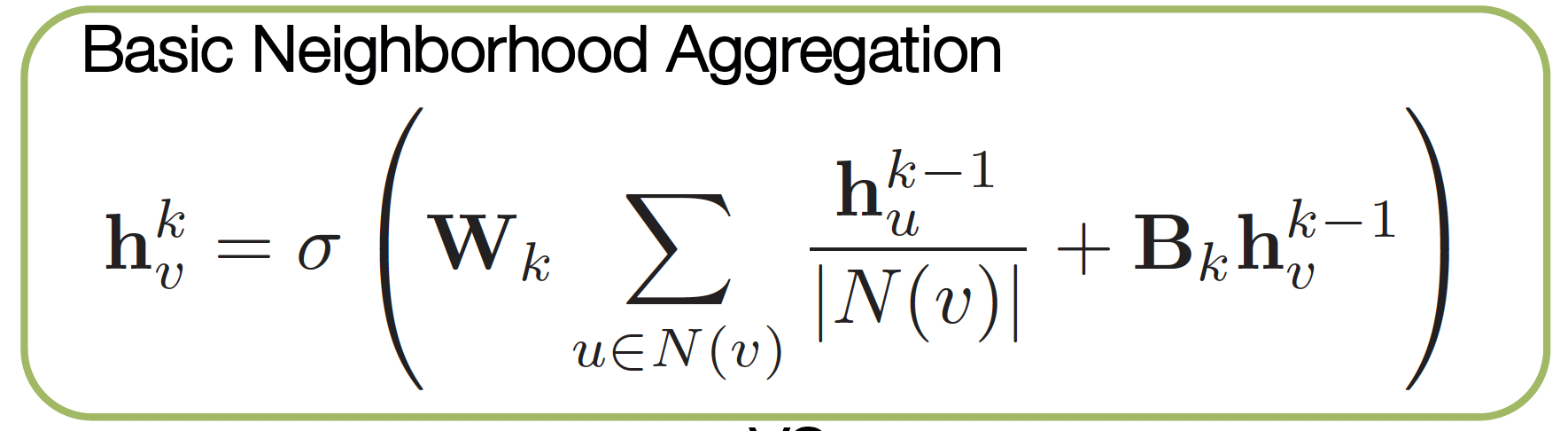
   Figure 3: Basic Neighborhood aggregation

Graph Convolutional Neural Networks

1. Parameter sharing between self and neighborhood embeddings

Figure 4: Graph Convolutional Network based Graph Aggregation

Disadvantages:

1. Need the whole graph laplacian!
2. Every step requires loading the whole graph into memory. We should sample graph neighborhoods.

Graph Sage (Sample and Aggregate)

1. Sample a neighborhood

   

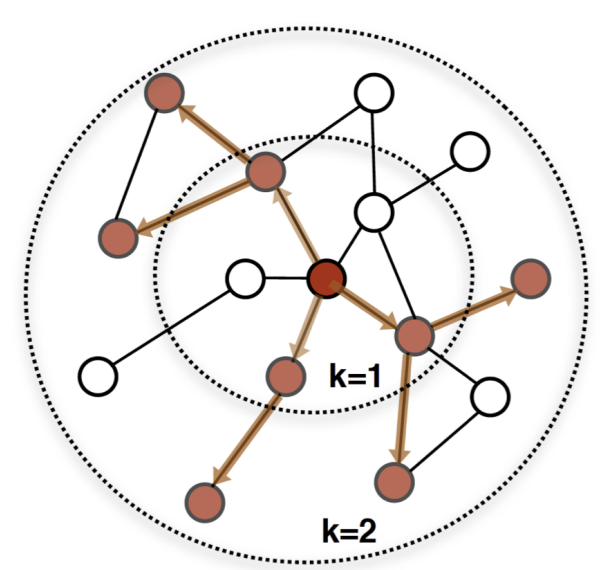
2. Aggregate across k neighborhoods (here, k=2)

   

3. Predict output based on context and label using g

   

4. Things to note:
   1. Aggregation function could be any kernel, for e.g.
      1. Simple Average
      2. Pooling
      3. LSTM (in the case of an evolving structure)
5. Advantages of this approach:
   1. Sampling means not requiring to load the whole graph.
   2. Variation across what can be the aggregation function.
   3. Very useful in scenarios where high throughput performance is requires on evolving graphs.

Few Applications

1. Citation Networks
   1. Goal is to predict paper subject categories.
2. Reddit posts classification (into subreddits)
   1. Connections based on user activity.

References

1. F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner, and G. Monfardini. The graph neural network model. IEEE Transactions on Neural Networks, 20(1):61–80, 2009
2. B. Perozzi, R. Al-Rfou, and S. Skiena. Deepwalk: Online learning of social representations. In KDD, 2014.
3. W. L. Hamilton, Z. Ying, and J. Leskovec, “Inductive representation learning on large graphs,” NIPS 2017, pp. 1024–1034, 2017
4. T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” ICLR 2017, 2017